Fijamos el eje x de un sistema de coordenadas, y su origen 0 según la figura. Sea N el
número de espiras, y L la longitud del solenoide.
número de espiras, y L la longitud del solenoide.
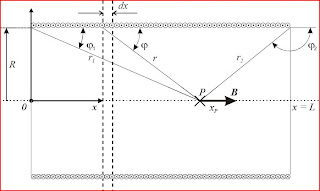
Calcularemos de una manera suficientemente exacta la intensidad del campo B en un punto
cualquiera P del eje geométrico.Podemos calcular el valor del campo magnético B en este punto considerando a cada espira aisladamente, y aplicando el principio de superposición. Para ello podemos tomar la distancia de cada espira al punto considerado, y calculando el valor del campo que cada espira individualmente aporta al punto P , al efectuar la sumatoria de los valores calculados sobre todas las espiras, podemos obtener el valor del campo resultante en P.
Ahora bien, como se darán cuenta, este procedimiento es sumamente laborioso, sobre todo considerando que existen solenoides que poseen varios miles de espiras.
cualquiera P del eje geométrico.Podemos calcular el valor del campo magnético B en este punto considerando a cada espira aisladamente, y aplicando el principio de superposición. Para ello podemos tomar la distancia de cada espira al punto considerado, y calculando el valor del campo que cada espira individualmente aporta al punto P , al efectuar la sumatoria de los valores calculados sobre todas las espiras, podemos obtener el valor del campo resultante en P.
Ahora bien, como se darán cuenta, este procedimiento es sumamente laborioso, sobre todo considerando que existen solenoides que poseen varios miles de espiras.
Necesitamos aplicar entonces, un método matemático que nos permita simplificar este
trabajo. A estos fines, nosotros podemos asociar todo este conjunto de espiras arrollada una al lado de la otra, por las cuales circula en cada espira el mismo valor de corriente i , y al tener todas el mismo diámetro, podemos asociar a una distribución “laminar” de corriente eléctrica en la superficie del cilindro sobre el cual está arrollado el solenoide. Luego, si nosotros tomamos la corriente que circula
trabajo. A estos fines, nosotros podemos asociar todo este conjunto de espiras arrollada una al lado de la otra, por las cuales circula en cada espira el mismo valor de corriente i , y al tener todas el mismo diámetro, podemos asociar a una distribución “laminar” de corriente eléctrica en la superficie del cilindro sobre el cual está arrollado el solenoide. Luego, si nosotros tomamos la corriente que circula
En cada espira y la multiplicamos por el número de espiras, tendríamos este valor de corriente laminar Ni. Con este concepto definimos una densidad lineal de corriente N·i/L. Haciendo esta aproximación podemos tomar una “fibra” de esta corriente laminar, como si fuera una espira elemental de espesor dx por la que circula una corriente (N·i/L)dx. Esto nos va a permitir integrar a lo largo del eje de la espira ya que con la aproximación matemática efectuada podemos dejar de considerar a las espiras en forma discretas, sino como un desarrollo continuo a lo largo de x. O sea, ya no tomamos a las espiras individualmente, sino al conjunto de espiras distribuidas a lo largo de la longitud L, como N/L, y a una fracción elemental de este conjunto como (N/L)dx.
Vamos entonces a calcular el valor de campo magnético que produce este paquete elemental
de espiras en el punto P. La expresión general de la Primera Ley elemental de Laplace-Ampère era en su forma escalar:
de espiras en el punto P. La expresión general de la Primera Ley elemental de Laplace-Ampère era en su forma escalar:

Cuando calculábamos el campo en el eje de una espira tomábamos el valor de la proyección
del campo en una dirección paralela al eje de la espira:

que es un diferencial de segundo orden en x (a lo largo del eje x), y en l (alrededor de la espira). Para resolver esto, debemos efectuar una doble integración, una por cada variable, x, y c :

del campo en una dirección paralela al eje de la espira:
Si a esta expresión la multiplicamos por (N/L)dx tenemos entonces el valor de campo B que
produce el elemento de corriente i.dc de una fracción elemental de espiras:

que es un diferencial de segundo orden en x (a lo largo del eje x), y en l (alrededor de la espira). Para resolver esto, debemos efectuar una doble integración, una por cada variable, x, y c :

Efectuamos una primera integral alrededor de la espira, o sea a lo largo de 2πR , dando
como resultado:
La intensidad total del campo B en el punto P será:

Dentro de la integral nos encontramos con tres variables diferentes pero no independientes.
El problema se reduce ahora a unificar las variables que se encuentran dentro de la expresión integral, para poder resolverla. Para ello tendremos en cuenta las siguientes consideraciones:
El problema se reduce ahora a unificar las variables que se encuentran dentro de la expresión integral, para poder resolverla. Para ello tendremos en cuenta las siguientes consideraciones:


diferenciando esta expresión, tenemos:

Cuando reemplazamos valores, nos queda ya, esta integral referida a una sola variable, el
ángulo ϕ . Resta ahora unificar los límites de la integral. Tenemos que para x = 0 , el ángulo
correspondiente es ϕ1, mientras que para x = L , el ángulo correspondiente es ϕ2:


Ahora bien, nosotros podemos detener aquí el cálculo; entonces la cuestión del campo en un
solenoide se va a reducir a hallar los valores de los ángulos ϕ1 y ϕ2. Pero si nosotros establecemos las relaciones trigonométricas de estos ángulos con las dimensiones del solenoide, podemos simplificar aún más, y generalizar mejor la expresión del campo. Para ello tenemos:
solenoide se va a reducir a hallar los valores de los ángulos ϕ1 y ϕ2. Pero si nosotros establecemos las relaciones trigonométricas de estos ángulos con las dimensiones del solenoide, podemos simplificar aún más, y generalizar mejor la expresión del campo. Para ello tenemos:

Con lo cual, al reemplazar estos valores en la expresión calculada del campo, nos queda:

que es la función que representa el valor del campo B , para cualquier punto que se encuentra sobre el eje de un solenoide, tanto dentro como fuera del mismo. Particularmente nos interesa hallar el valor del campo en puntos típicos del eje del solenoide. Uno de ellos es el punto medio del solenoide que, nos damos cuenta, es donde el campo B adquiere su mayor valor sobre el eje. Otros puntos interesantes de calcular son los dos puntos extremos del solenoide. Para el punto medio del eje del solenoide, Xp = L/2 por lo que la ecuación se reduce a:

Para los dos extremos del solenoide, podemos ver que al reemplazar xP = 0 , ó xP = L
en la expresión el campo B adquiere el mismo valor, lo cual se justifica por cuestiones de simetría.

Tenemos entonces ya, calculado el campo B en dos puntos típicos del eje del solenoide.
Estas expresiones de campo son válidas para cualquier tipo de solenoide, particularmente en los casos en que el largo del mismo no sea apreciable frente a su radio (hasta 10R ); los mismos se denominan solenoide corto. Cuando el solenoide está formado por más de una capa de espiras, se adoptará para efectuar los cálculos, el radio medio (o promedio) de dichas capas de espiras; se deberá tener en cuenta que, cuando se aumenta el número de capas, aumenta la incertidumbre del resultado5. Lo mismo ocurre cuando disminuye el número de espiras, o se incrementa el espaciado entre las mismas (aumenta el paso de la helicoide).
Estas expresiones de campo son válidas para cualquier tipo de solenoide, particularmente en los casos en que el largo del mismo no sea apreciable frente a su radio (hasta 10R ); los mismos se denominan solenoide corto. Cuando el solenoide está formado por más de una capa de espiras, se adoptará para efectuar los cálculos, el radio medio (o promedio) de dichas capas de espiras; se deberá tener en cuenta que, cuando se aumenta el número de capas, aumenta la incertidumbre del resultado5. Lo mismo ocurre cuando disminuye el número de espiras, o se incrementa el espaciado entre las mismas (aumenta el paso de la helicoide).
Escrito por Jorge Alcaíno

